How Transformers Learn Order: Absolute, Relative, and Rotary Positions

Transformers process tokens in parallel and have no built‑in sense of order.
Positional encodings inject information about where each token appears in the sequence.

The basic idea: each position gets a vector, and that vector is added to the token embedding before entering the transformer. This lets the model distinguish sequences like “dog bites man” from “man bites dog” and learn how order affects meaning.

Over time, several approaches to positional encoding have emerged, ranging from fixed sinusoidal schemes to fully learned embeddings, relative encodings, and rotary methods, each with different tradeoffs in flexibility, inductive bias, and length generalization.

1. Sinusoidal Positional Encoding

Sinusoidal positional encoding, introduced in Attention Is All You Need (2017), uses sine and cosine functions at different frequencies to represent each position.

For position \(pos\), embedding dimension \(i\), and \(d_{model}\) as the embedding dimension:

Given input embeddings \(X \in \mathbb{R}^{L \times d}\):

• Queries: \(Q = X W^Q\)
• Keys: \(K = X W^K\)
• Values: \(V = X W^V\)

These position vectors are added to the inputs before computing queries, keys, and values:

Interestingly, lower dimensions change slowly with position and capture coarse trends, while higher dimensions oscillate faster and capture fine-grained differences.

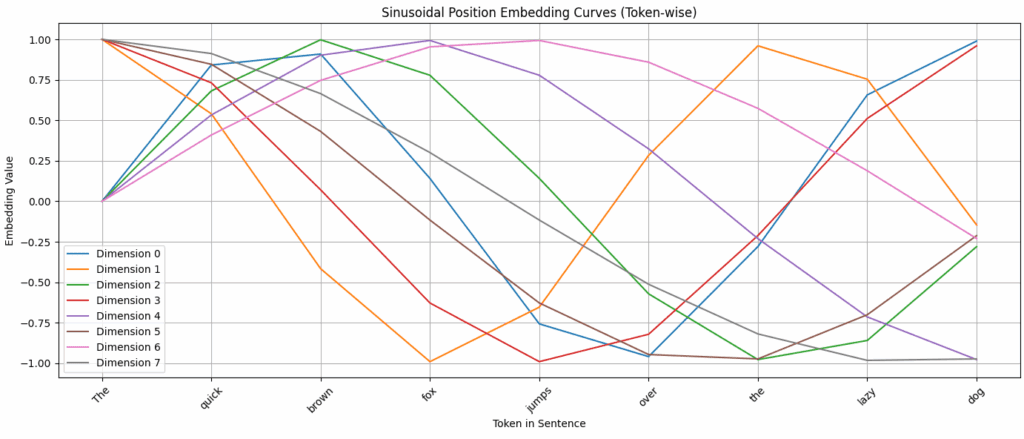
Limitations:

1. Generalization to much longer sequences is limited; the periodic nature can cause positional ambiguity.
2. The encodings are fixed and do not adapt to the data.
3. They cannot adjust dynamically to shifts in positions or varying sequence lengths at inference time.

These issues motivated learned and relative positional methods.

2. Learnable Positional Encodings

Learnable positional encodings use an embedding table whose values are trained along with the rest of the model. This lets the model adapt positional representations to the task and data. They can be especially effective when absolute positions matter.

Their main limitations is adding parameters and can overfit on small or narrow datasets.

class LearnedPositionalEmbedding(nn.Module):
    def __init__(self, max_len: int, d_model: int):
        super().__init__()
        self.pos_embed = nn.Embedding(max_len, d_model)

    def forward(self, x):
        # x: (batch, seq_len, d_model)
        seq_len = x.size(1)
        positions = torch.arange(seq_len, device=x.device).unsqueeze(0)
        return self.pos_embed(positions)  # (1, seq_len, d_model)

Relative Positional Encoding

Relative positional encodings represent distances between query and key positions instead of absolute indices. This often helps when relative order matters more than absolute position (language modeling, local patterns).

Relative encodings often come in two flavors: adding positional information to the keys only, or adding it to both keys and values.

• \(A^K \in \mathbb{R}^{L \times L \times d_z}\) added to keys
• \(A^V \in \mathbb{R}^{L \times L \times d_z}\) added to values

Attention becomes:

While these methods work well, their main drawback is that the pairwise bias tensors are memory‑heavy for long sequences. In addition, they do not, by themselves, encode absolute position information, which can be limiting when absolute anchors (like “start” or “end” of the sequence) matter.

Rotary Positional Embeddings (RoPE)

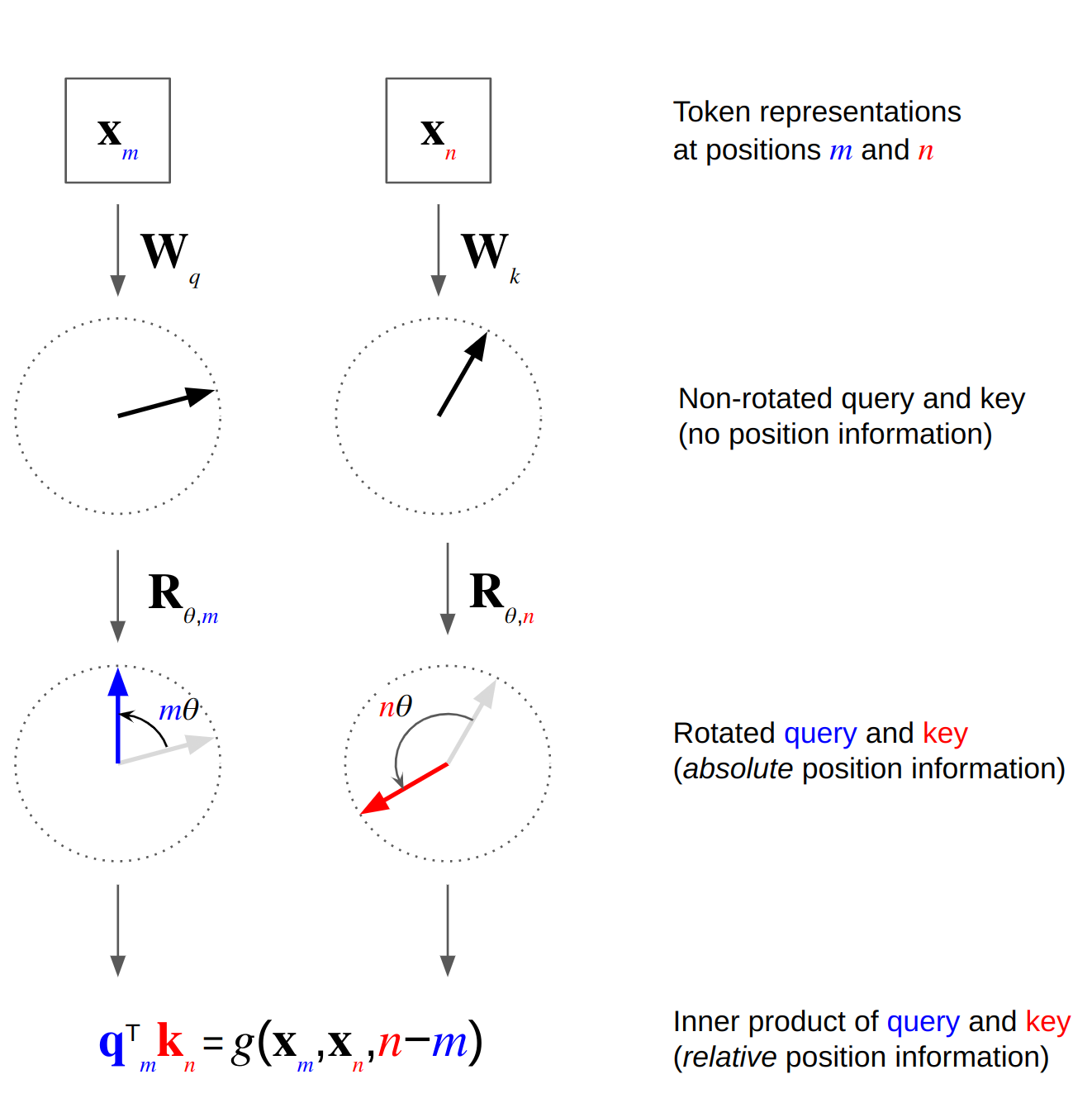
Rotary Positional Embeddings (RoPE) encode position by rotating embeddings in 2D subspaces, with rotation angles that grow with the token index.

Conceptually, split each token’s embedding into pairs of dimensions. RoPE applies a 2D rotation to each pair using an angle proportional to the token’s position. When attention computes dot products between the rotated queries and keys, the result depends on the difference in their rotation angles. This makes the attention scores sensitive to relative positions, while the embeddings themselves still carry absolute position information.

For a sequence of length \(L\), token position \(m \in [0, L - 1]\), and head dimension \(d_z\), consider dimension pair \((2i, 2i+1)\) of the query and key vectors \(q_m, k_m \in \mathbb{R}^{d_z}\). RoPE transforms the query as:

and the keys as:

with frequency term

Attention is then computed using the rotated queries and keys:

By properties of rotation matrices, the dot product between two rotated vectors at positions \(m\) and \(n\) can be written as:

where \(R_{n-m}\) is a rotation matrix that depends only on the relative offset \(n - m\). This makes the attention scores explicitly depend on relative positions, while still using absolute indices in the construction of \(\hat{q}_m\) and \(\hat{k}_m\).

def apply_rope(x):
    # x: (batch, seq_len, n_heads, head_dim)
    batch_size, seq_len, n_heads, head_dim = x.shape
    assert head_dim % 2 == 0, "head_dim must be even for paired rotation"

    dim = head_dim // 2
    inv_freq = 1.0 / (10000 ** (torch.arange(0, dim).float() / dim))
    positions = torch.arange(seq_len, device=x.device).float()

    angle_rates = torch.einsum('i,j->ij', positions, inv_freq)  # (seq_len, dim)

    sin_angles = angle_rates.sin()[:, None, :]  # (seq_len, 1, dim)
    cos_angles = angle_rates.cos()[:, None, :]  # (seq_len, 1, dim)

    x1, x2 = x[..., :dim], x[..., dim:]

    x_rotated_first = x1 * cos_angles - x2 * sin_angles
    x_rotated_second = x1 * sin_angles + x2 * cos_angles

    x_rotated = torch.cat([x_rotated_first, x_rotated_second], dim=-1)
    return x_rotated

Comparing the Methods

• Positional information is mandatory for transformers; without it, they cannot model order.
• Sinusoidal: Simple, parameter-free, and can extrapolate somewhat beyond training lengths.
• Learned absolute: Good when sequence length is fixed and you want simplicity and task-specific adaptation.
• Relative encodings: Strong when local relative structure matters and for longer-context generalization.
• RoPE: Popular in modern LLMs because it naturally encodes relative positions, works well at scale, and supports long-context extensions with appropriate scaling tricks.

Practical Notes

• Most models add positional encodings to token embeddings. Some use concatenation or separate bias terms.
• Learned absolute embeddings have a hard maximum length. Sinusoidal, relative, and RoPE-style methods typically extrapolate better.
• When adding positional encodings, the relative scale matters. Some implementations rescale embeddings or apply layer normalization for stability.
• Relative methods can add a bit of overhead (extra lookups or kernels) but often improve performance.

Resources

Sinusoidal Encodings

• Attention Is All You Need
• Inside Sinusoidal Position Embeddings: A Sense of Order

Relative Positional Encodings

• Relative Positional Encoding
• Self-Attention with Relative Position Representations

Rotary Positional Embeddings (RoPE):

• How Rotary Position Embedding Supercharges Modern LLMs (RoPE)
• A gentle introduction to Rotary Position Embedding
• RoFormer: Enhanced Transformer with Rotary Position Embedding