Attention Layer

Attention blocks are the backbone of the Transformer architecture, enabling the model to capture dependencies across the input sequence.

An attention layer takes as input:

  1. A query vector \(q \in \mathbb{R}^d\)
  2. A matrix of keys \(K \in \mathbb{R}^{n \times d}\) (rows are \(k_i^\top\))
  3. A matrix of values \(V \in \mathbb{R}^{n \times d_v}\)

In the vanilla Transformer setup, the query, key, and value come from the same token embedding \(x\) but the model is free to learn different subspaces for “asking” (queries), “addressing” (keys), and “answering” (values):

  • \(q = xW^Q\)
  • \(k = xW^K\)
  • \(v = xW^V\)

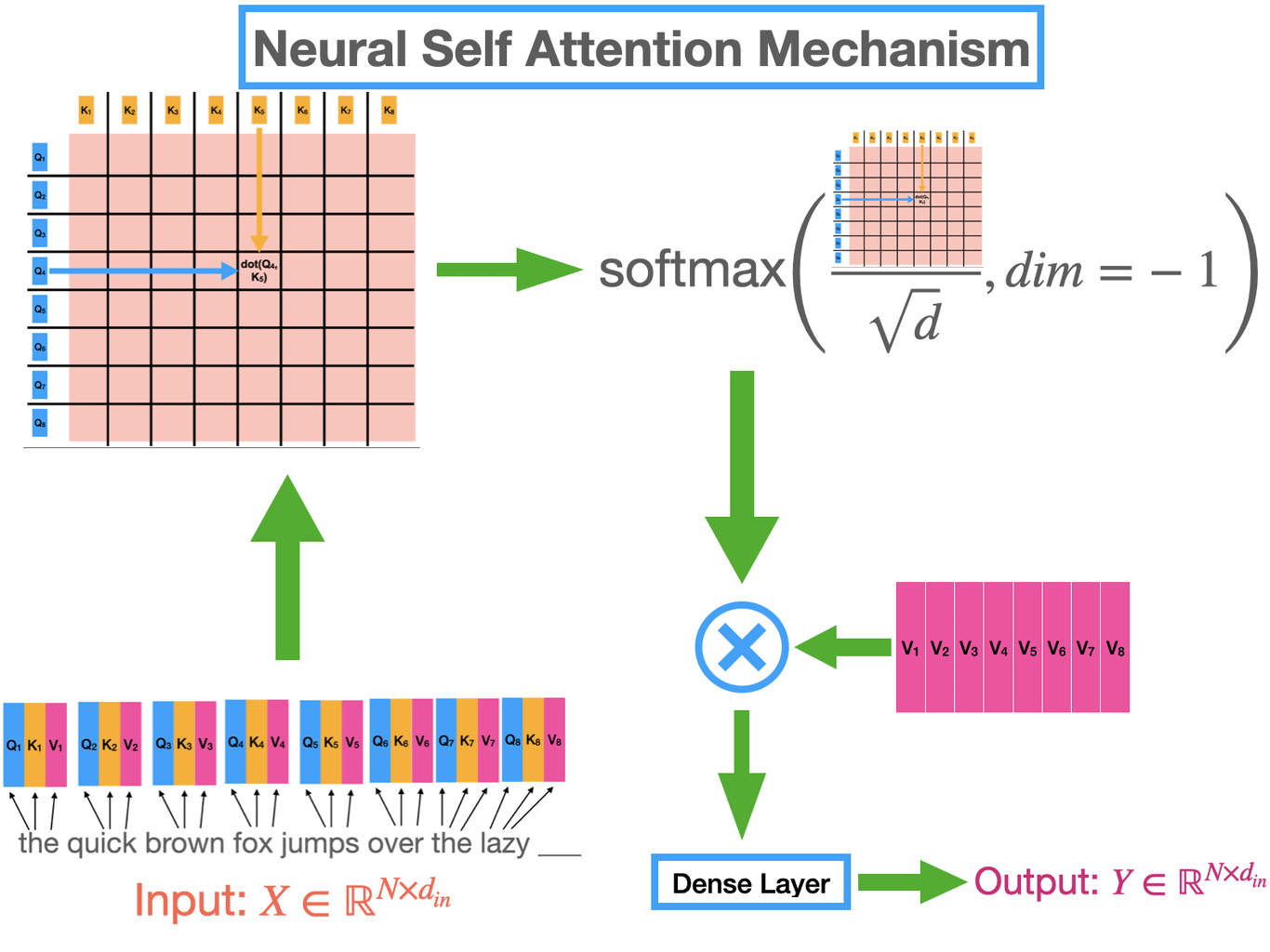
Then, to compute the attention the following procedure is executed:

  1. Compute similarities: $$ s_i=\frac{\langle q,k_i\rangle}{\sqrt{d}} $$
  2. Convert scores to probabilities: $$ p_i=\mathrm{softmax}(s)_i=\frac{e^{s_i}}{\sum_j e^{s_j}} $$
  3. Aggregate values: $$\mathrm{Attn}(q,K,V)=\sum_{i=1}^n p_i\, v_i$$

For a batch of queries $Q\in\mathbb{R}^{m\times d}$:

$$ \mathrm{Attn}(Q,K,V)=\mathrm{softmax}\!\Big(\frac{QK^\top}{\sqrt d}\Big) V \quad\text{(row-wise softmax).} $$

With tokens as nodes, attention does content-based weighted aggregation—like a fully connected Graph-Neural-Network (GNN) layer with learned edge weights.

Attention Taken from https://learnopencv.com/attention-mechanism-in-transformer-neural-networks/

Why $\tfrac{1}{\sqrt d}$ scaling?

If \(q,k_i\sim\mathcal N(0,I)\), then \(\langle q,k_i\rangle\) has variance \(d\):

$$ \begin{aligned} Var(\langle q,k_i\rangle) &= E\left[(\langle q,k_i\rangle-0)^2\right] = E\left[\left( \sum_{n=1}^d q_n \cdot k_{in}\right)^2\right] \ &= E\left[\sum_{n=1}^d q_n^2 k_{in}^2 ;+; 2\sum_{1\le n<m\le d} q_n k_{in}, q_m k_{im}\right] \ &= \sum_{n=1}^d E\left[ q_n^2\right] E\left[k_{in}^2\right] \ &=d \end{aligned}

$$

where we used the following properties:

  1. $\mathbb{E}[q_n]=\mathbb{E}[k_{in}]=0$.
  2. Independence across coordinates and between $q$ and $k$.
  3. $\mathbb{E}[q_n^2]=\mathbb{E}[k_{in}^2]=1$.

Dividing by \(\sqrt d\) keeps the variance of the logits near 1, preventing softmax saturation and stabilizing gradients.

Multi-Head Attention

Multi-head attention combines multiple low-rank bilinear forms, making it expressive yet parameter-efficient. Each head corresponds to a different kernel (or subspace), yielding disentangled relational channels and richer low-rank structure.

The model learns \(h\) sets of projections, each of dimension \(d_h = d/h\):

  • \(QW_i^Q \)
  • \(KW_i^K\)
  • \(VW_i^V\),

It computes \(h\) separate attentions in parallel, concatenates the results, and projects them with \(W^O\).

Causal/masked attention: A mask \(M\) with \(-\infty\) on disallowed positions is added before softmax:

$$ \mathrm{softmax}\!\Big(\frac{QK^\top}{\sqrt d} + M\Big)V. $$

Compute and Storage Cost

For seq length \(n\), width \(d\) (each token in the sequence is represented by a vector of length \(d\)), the cost is

  • \(O(n^2 d)\) compute
  • \(O(n^2)\) memory (the attention matrix)

This motivates long-context variants (sparse, linearized, low-rank, etc.).

In Linear attention, the softmax kernel is replaced by a feature map \(\phi(\cdot)\) with $\kappa(q,k)\approx \phi(q)^\top\phi(k)$ to get

$$ (\phi(Q)\,(\phi(K)^\top V)) $$

and \(O(n d^2)\) time, \(O(n d)\) memory.

In KV caching (inference), past $K,V$ are re-used to serve next query in $O(n d)$ per step.

Resource

https://learnopencv.com/attention-mechanism-in-transformer-neural-networks/