TL;DR
Recent advancements in vector retrieval demonstrate that mapping queries and documents to multiple vectors and performing multi-vector retrieval surpasses common single-vector retrieval methods. However, multi-vector retrieval is computationally intensive as it does not use linear operations like the inner product. MUVERA is a method designed to accelerate multi-vector retrieval: It converts sets of vectors into single Fixed Dimensional Encodings (FDEs). The inner product of two FDEs approximates the Chamfer Similarity score, allowing standard, highly-optimized Maximum Inner Product Search (MIPS) solvers to generate a candidate list, following by exact similarity calculation on this small set of candidates for precise ranking.
Motivation
Models like ColBERT generate a set of embeddings for each document or query, often one vector per token. This approach has shown improved performance on information retrieval benchmarks. The similarity between a query set of vectors \(Q = \{q_1, \dots, q_n\}\) and a document set \(D = \{d_1, \dots, d_m\}\) is calculated using Chamfer Similarity (also called MaxSim). This involves finding the best-matching document vector for each query vector and summing the similarity scores.
$$ \text{ChamferSimilarity}(Q, D) = \sum_{i=1}^{n} \max_{j=1, \dots, m} \text{similarity}(q_i, d_j) $$This calculation presents two primary challenges:
- Representing each token as a vector increases the total number of embeddings in a corpus by a large factor (storage cost)
- The MaxSim operation is non-linear and cannot be optimized with standard inner product search indexes (computational cost)
MUVERA aims to create a simpler, faster alternative that maps the problem back to a standard single-vector search paradigm.
Method: Multi-Vector Retrieval Algorithm
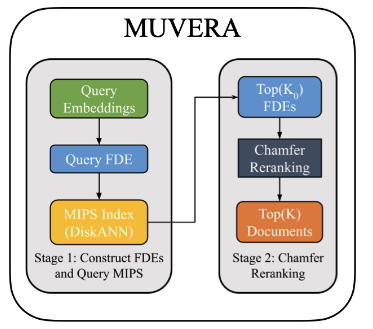
MUVERA is a two-stage retrieval process that uses FDEs to approximate Chamfer Similarity for fast candidate generation. In its core is FDE: a single vector constructed from a set of vectors through a data-oblivious transformation. This makes the encoding process fast and robust to data distribution shifts.
MUVERA creates and utilizes FDEs as follows.
- Partitioning: The embedding space is randomly partitioned into \(B\) disjoint regions or clusters.
- Aggregation: Vectors within each partition are aggregated differently for queries and documents to reflect the asymmetry of Chamfer Similarity.
- Query FDEs: All query vectors falling into a partition are summed.
- Document FDEs: All document vectors falling into a partition are averaged. If a partition contains no document vectors, a
fill_empty_clusterstechnique can be used to assign it the vector from the document closest to that partition’s center.
- Projection: To manage dimensionality and improve robustness, a random linear projection is applied to the aggregated vector in each partition, reducing it to a dimension of \(d_{proj}\).
- Repetition This entire process (partitioning, aggregation, projection) is repeated \(R_{reps}\) times with different random seeds, and the resulting vectors are concatenated.
The final FDE has a dimension of \(B \cdot d_{proj} \cdot R_{reps}\).
Limitations
- The method’s effectiveness depends on how well the FDE inner product approximates Chamfer Similarity. This relationship is controlled by hyperparameters ( \(B, d_{proj}, R_{reps}\) ), creating a trade-off between the FDE dimension (and thus speed/memory) and retrieval accuracy.
- While faster, MUVERA requires storing an additional FDE vector for each document. The size of this vector can become large depending on the hyperparameter settings, which may be a constraint in memory-limited environments.
- Although robustness is a strength, a data-oblivious partitioning scheme may be less optimal than a data-aware one (e.g., k-means clustering).