TL;DR
Chain-of-Thought (CoT) enables large language models (LLMs) to solve complex tasks by generating intermediate reasoning steps. Ada-R1 approach fine-tunes a model to prefer Short-CoT over Long-CoT based on problem complexity, using training a model to minimize reasoning length while preserving accuracy. This approach reduces average reasoning length by over 50%, substantially lowering inference cost, with maintained accuracy across five mathematical reasoning benchmarks.
Background
CoT prompting decomposes complex tasks into intermediate reasoning steps.
This improves interpretability and performance on reasoning benchmarks.
Long-CoT produces detailed, stepwise derivations suited for multi-step problems while Short-CoT yields concise justifications for simpler tasks.
Uniform application of Long-CoT increases inference latency and resource use and also may also degrade performance on straightforward problems.
Ada-R1 leverages both Long-CoT and Short-CoT capabilities by adaptively selecting reasoning depth according to problem complexity.
Motivation.
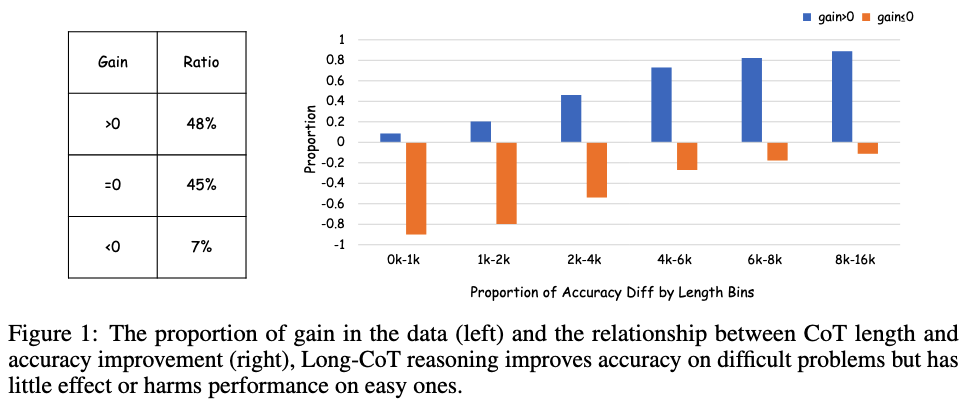
The authors compare DeepSeek-R1-Distill-Qwen-7B (Long-CoT) and its fine-tuned variant with 2K Short-CoT samples from Qwen2.5-Math-7B-Instruct.
Across 2K problems, 12 responses per model per question are generated, excluding cases where both models fail.
Accuracy gains are computed as the difference between Long-CoT and Short-CoT.
Results show that for about half the samples, Long-CoT offers no benefit and sometimes reduces accuracy.
Method
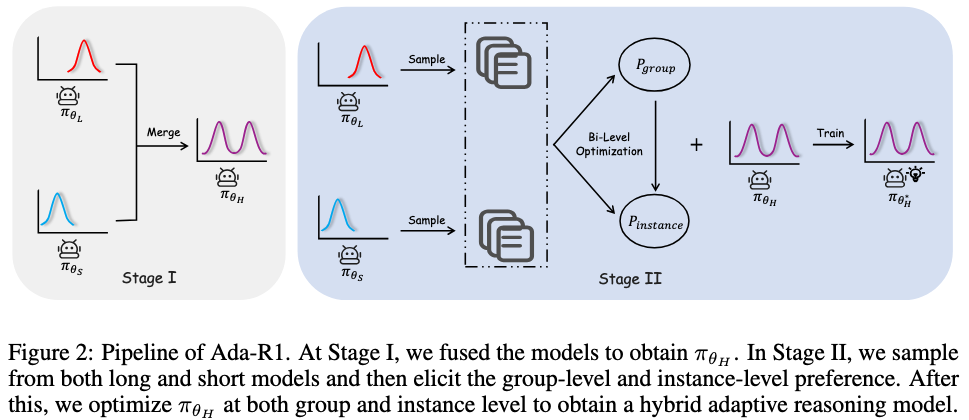
Ada-R1 employs a two-stage adaptive reasoning framework:
Stage I: Long-and-Short Reasoning Merge. Long-CoT and Short-CoT models are combined via linear parameter interpolation. This enables the hybrid model to generate either detailed or concise reasoning as required.
Stage II: Bi-Level Preference Training.
Training comprises:
- Group-Level Preference: The model learns to select the optimal reasoning style (Long-CoT or Short-CoT) based on expected correctness.
- Instance-Level Preference: Within each style, the model is trained to prefer the most concise correct response.
To create the training dataset, for each problem in a Math dataset, K solutions are sampled from both models. Training pairs are formed from the Cartesian product of these groups. A subset is used to construct DPO training tuples (x, yw, yl), where x is the anser, yw is the preferred response.
Instance-level preferences further encourage brevity among correct responses within each group.
Limitations
Bi-Level Preference Training requires sampling many candidate chains and labeling them by correctness and CoT length. Generating this data is compute-intensive, and the learned preferences may not transfer to new domains without re-sampling and re-labeling.