TL;DR
Oversmoothing is a common phenomenon in Transformers, where performance worsens due dimensional collapse of representations, where representations lie in a narrow cone in the feature space. The authors analyze the Contrastive lose and extracted the term that prevent this collapse. By taking a gradient descent step with respect to the feature later, they come up with the ContraNorm layer that leads to a more uniform distribution and prevents the dimensional collapse.
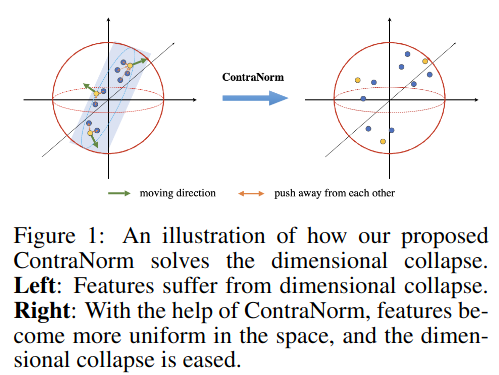
On dimension collapse in Transformers
Representation collapse in Transformers occurs when deeper layers cause features to lose expressivity, leading to performance decline. This phenomenon is usually measured using attention map similarity: as attention map similarity converges to one, feature similarity increases.
However, using the attention map similarity overlooks cases of dimensional collapse: it fails to capture cases where representations span a low-dimensional space without fully collapsing.
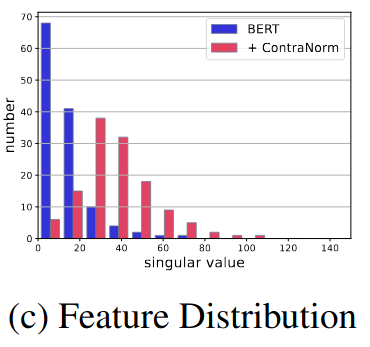
The figure below shows the singular values distribution. It illustrates how the proposed method helps to distribute singular values more uniformly across dimensions.
Method
The ContraNorm is proposed to mitigate the dimensional collapse in Transformers by applying the following transformation:
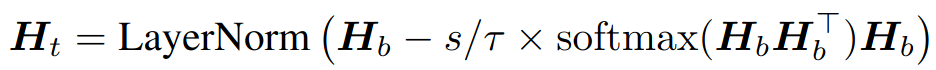
- \(H_b\) is the feature matrix
- \(\tau\) is the temperature scaling
- \(s\) is an hyper-parameter corresponds to the gradient descent step
Deriving the ContraNorm layer. Looking at the contrastive loss, it can be decoupled into alignment loss and uniformity loss
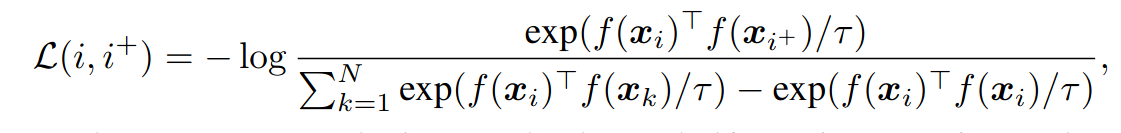
- The alignment loss (the numerator) encourages feature representations for positive pairs to be similar, thus being invariant to unnecessary noises. However, training with only the alignment loss will result in a trivial solution where all representations are identical.
- The uniformity loss (the denominator) maximizes average distances between all samples, resulting in embeddings that are roughly uniformly distributed in the latent space.
An alternative approach to address oversmoothing is to directly incorporate the uniformity loss into the training objective. However, experiments shows that this method has limited effectiveness Instead, a normalization integrated into the model:
- Taking the derivative of the uniformity loss
- Apply a single step of gradient descent
- In addition, LayerNorm(*) is applied on top to guarantee a more uniform distribution of the features in each update step.
Limitations
- The method introduces three additional hyperparameters: (i) the uniformity strength, (ii) temperature scaling, and (iii) LayerNorm parameters.
- While ContraNorm helps alleviate dimensional collapse, there may be a trade-off between reducing collapse and maintaining feature diversity. Preventing the model to compress the input may slow down the model convergence.
Resources
arxiv, published in ICLR 2023